z3-solver求解器

z3-solver是由Microsoft Research(微软)开发的SMT求解器，它用于检查逻辑表达式的可满足性，可以找到一组约束中的其中一个可行解，缺点是无法找出所有的可行解

pip安装：pip install z3-solver

基本用法：

1
2
3
4
5
6
7
8
9
import z3
x.Int('x')
y.Int('y')
s=z3.Solver()
s.add(x+y=4)
if s.check() == z3.sat:
    print(s.model())
else:
    raise Exception("NO SOLUTION!")

实数：y = z3.Real(name = 'y')

位向量：z = z3.BitVec(name = 'z', bv = 32)

布尔：p = z3.Bool(name = 'p')

对于布尔类型的式子而言，我们可以使用 z3 内置的 And()、Or()、Not()、Implies() 等方法进行布尔逻辑运算

例题

[NSSRound#X Basic]ez_z3

第一步查壳，是64位，UPX的魔改壳，把XYU改成UPX后直接脱壳

第二步放入ida找到关键代码

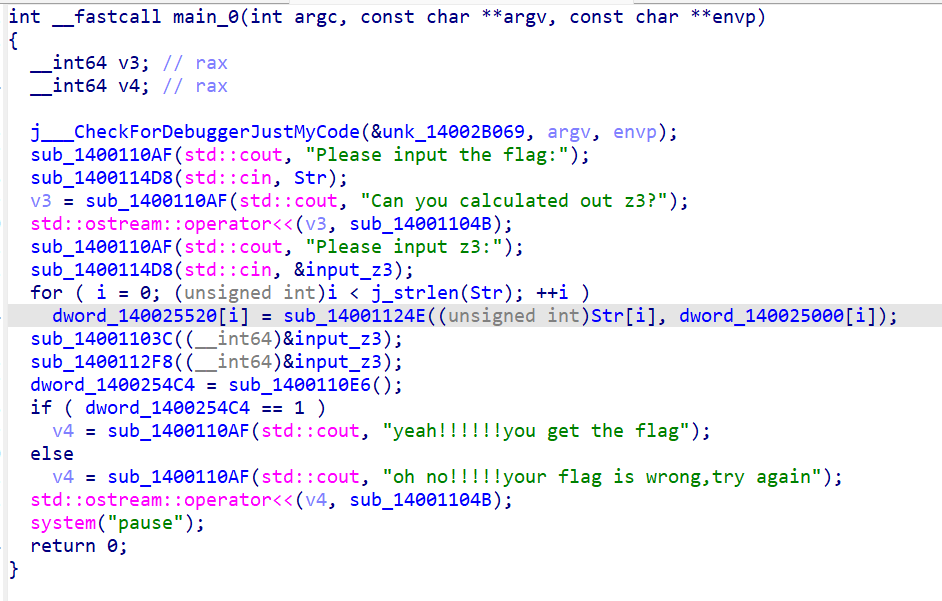
daima

sub_14001124E函数是快速幂的变体，

sub_14001103C里面一堆方程，用z3求解，但是ida代码中方程直接的逻辑关系是||，但是只有全部满足才能做出来，有点奇怪

sub_1400112F8是异或，最后判断是否相等

exp:

求z3

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
from z3 import *
s=Solver()
a0,a1,a2,a3,a4,a5,a6,a7,a8,a9 = BitVecs("a0 a1 a2 a3 a4 a5 a6 a7 a8 a9",12)
a10,a11,a12,a13,a14,a15,a16,a17,a18,a19 = BitVecs("a10 a11 a12 a13 a14 a15 a16 a17 a18 a19",12)
s.add(2582239 == a0*1 + a1*2 - a2*3 - a3*4 + a4*5 + a5*6*5 - a6*7 + a7*8 - a8*9 + a9*10
* a10*11 - a11*12 + a12*13 + a13*14 - a14*15 * a15*16 - a16*17 - a17*18 + a18*19 * a19*20)
s.add(2602741 == a0*1 * a1*2 + a2*3 - a3*4 + a4*5 + (a5*6*5 - a6*7 + a7*8 - a8*9) + a9*10
* a10*11 - a11*12 + a12*13 + a13*14 - a14*15 * a15*16 - (a16*17 + a17*18) + a18*19 *
a19*20)
s.add(2668123 == a0*1 - a1*2 - a2*3 * a3*4 - a4*5 + a5*6*5 * a6*7 + a7*8 + a8*9 - a9*10
+ a10*11 * a11*12 + a12*13 * a13*14 - a14*15 - a15*16 * a16*17 + a17*18 + a18*19 -
a19*20)
s.add(2520193 == (a0*1 + a1*2 - a2*3 - a3*4 + a4*5) + a5*6*5 - a6*7 + a7*8 - a8*9 + a9*10
* (a10*11 - a11*12 + a12*13) + a13*14 - a14*15 * a15*16 - a16*17 - a17*18 + a18*19 *
a19*20)
s.add(8904587 == a0*1 * a1*2 * a2*3 - a3*4 - a4*5 - a5*6*5 - a6*7 + a7*8 * a8*9 + a9*10 -
a10*11 + a11*12 * a12*13 - a13*14 + a14*15 - a15*16 + a16*17 + a17*18 - a18*19 - a19*20)
s.add(1227620874 == a0*1 - a1*2 - a2*3 + (a3*4 + a4*5 * a5*6*5 * a6*7 + a7*8) - a8*9 -
a9*10 * a10*11 - (a11*12 + a12*13 - a13*14 - a14*15) * a15*16 - a16*17 + a17*18 - a18*19
- a19*20)
s.add(1836606059 == a0*1 + a1*2 + a2*3 + a3*4 + a4*5 + a5*6*5 * a6*7 + a7*8 - a8*9 +
a9*10 * a10*11 * a11*12 + a12*13 + a13*14 - a14*15 * a15*16 + a16*17 - a17*18 + a18*19
* a19*20)
s.add(8720560 == a0*1 * a1*2 - a2*3 + a3*4 + a4*5 + a5*6*5 * a6*7 + a7*8 - a8*9 - a9*10
- a10*11 + a11*12 + a12*13 + a13*14 + a14*15 * a15*16 - a16*17 - a17*18 + a18*19 *
a19*20)
s.add(11387045 == a0*1 + a1*2 - a2*3 + (a3*4 + a4*5 + a5*6*5 - a6*7 + a7*8 - a8*9 +
a9*10) * a10*11 - a11*12 + a12*13 + a13*14 - a14*15 * (a15*16 - a16*17 - a17*18) + a18*19
* a19*20)
s.add(7660269 == a0*1 - a1*2 + a2*3 + a3*4 - a4*5 - a5*6*5 - a6*7 + a7*8 + a8*9 + a9*10
* a10*11 - a11*12 - a12*13 + a13*14 + a14*15 * a15*16 - a16*17 - a17*18 + a18*19 * a19*20)
s.add(2461883 == a0*1 + a1*2 - (a2*3 * a3*4 - a4*5 - a5*6*5) - a6*7 + a7*8 - a8*9 + (a9*10
* a10*11 - a11*12) + a12*13 + a13*14 - a14*15 * a15*16 - a16*17 - a17*18 + a18*19 *
a19*20)
s.add(-966296 == a0 * 1 * a1 * 2 - a2 * 3 * a3 * 4 - a4 * 5 - a5 * 6 * 5 + a6 * 7 + a7 * 8 * a8
* 9 + a9 * 10 * a10 * 11 - a11 * 12 - a12 * 13 + a13 * 14 - a14 * 15 - a15 * 16 * a16 * 17 -
a17 * 18 - a18 * 19 - a19 * 20)
s.add(254500223 == a0*1 + a1*2 * (a2*3 + a3*4 + a4*5 + a5*6*5 - a6*7 + a7*8 - a8*9 +
a9*10 * a10*11) - a11*12 + a12*13 + a13*14 - a14*15 - a15*16 - a16*17 - a17*18 - a18*19
* a19*20)
s.add(6022286 == a0*1 - a1*2 - a2*3 - a3*4 * a4*5 + a5*6*5 * a6*7 + a7*8 - a8*9 + a9*10 *
a10*11 - a11*12 - a12*13 + a13*14 + a14*15 * a15*16 - a16*17 - a17*18 - a18*19 - a19*20)
s.add(-636956022 == a0 * 1 * a1 * 2 + (a2 * 3 * a3 * 4 + a4 * 5 + a5 * 6 * 5) - a6 * 7 * a7 * 8
* a8 * 9 + a9 * 10 * a10 * 11 + a11 * 12 - a12 * 13 + a13 * 14 - a14 * 15 + (a15 * 16 - a16 *
17 + a17 * 18) - a18 * 19 - a19 * 20)
s.add(10631829 == a0*1 * a1*2 * a2*3 - a3*4 + a4*5 + a5*6*5 + a6*7 - a7*8 * a8*9 + a9*10
* a10*11 + a11*12 + a12*13 - a13*14 - a14*15 - a15*16 - a16*17 - a17*18 + a18*19 *
a19*20)
s.add(6191333 == a0*1 + a1*2 + a2*3 * (a3*4 - a4*5 - a5*6*5) + a6*7 + a7*8 - a8*9 + (a9*10
* a10*11 - a11*12 + a12*13) + a13*14 * a14*15 + (a15*16 - a16*17 - a17*18) + a18*19 *
a19*20)
s.add(890415359 == a0*1 * a1*2 + a2*3 * a3*4 + a4*5 - a5*6*5 * a6*7 + a7*8 * a8*9 * a9*10
- a10*11 - a11*12 * a12*13 + a13*14 - a14*15 * a15*16 - a16*17 * a17*18 - a18*19 * a19*20)
s.add(23493664 == a0*1 + a1*2 * a2*3 * a3*4 - a4*5 + a5*6*5 - a6*7 + a7*8 + (a8*9 + a9*10
+ a10*11) + a11*12 - a12*13 - a13*14 - a14*15 + (a15*16 - a16*17 + a17*18 + a18*19 +
a19*20))
s.add(1967260144 == a0*1 + a1*2 * a2*3 - a3*4 - a4*5 + a5*6*5 * a6*7 * a7*8 - a8*9 + a9*10
- a10*11 + a11*12 + a12*13 - a13*14 - a14*15 * a15*16 - a16*17 - a17*18 + a18*19 *
a19*20)
if s.check() == sat:
    ans = s.model()
    print(ans)

爆破flag:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
a1 = [104, 97, 104, 97, 104, 97, 116, 104, 105, 115, 105, 115, 102, 97, 99, 107, 102, 108, 97, 103]
key = [7, 7, 7, 9, 5, 6, 7, 7, 7, 9, 7, 7, 5, 7, 7, 7, 5, 7, 9, 7]
ans = [4615, 19616, 20257, 57, 107811, 570, 2342, 19623, 25952, 54, 108955, 19624, 113632, 14085, 2342, 30675, 39576,25979, 24, 2833]

str = [0] * 20
d = [0] * 20


def power(x, y):
    v4 = 1
    v6 = y
    while v6:
        if (v6 & 1) != 0:
            v4 *= x
        x = x * x % 1000
        v6 >>= 2
    return v4


def inverse_power(v4, y):
    for x in range(32,127):  # 枚举可能的 x
        if power(x, y) == v4:
            return x


for i in range(20):
    d[i] = a1[20 - i - 1] ^ ans[i]
    str[i] = inverse_power(d[i], key[i])

for i in range(20):
    print(chr(str[i]),end='')